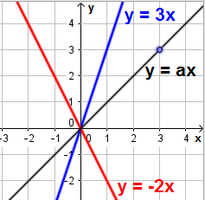
Võrdelise seos Seos kahe muutuja (näiteks x ja y) vahel, kus muutujate jagatis on alati sama.

${{y \over x} = a}$;
y = ax,
arv a on võrdetegur.
Pöördvõrdelise seos Seos kahe muutuja (näiteks x ja y) vahel, kus muutujate korrutis on alati sama.

xy = a;
${y = {a \over x}}$,
a on arv.
Lineaarne seos (lineaarfunktsioon) Seos kahe muutuja (näiteks x ja y) vahel, mis on esitatav kujul:

y = ax + b,
ax - lineaarliige, arv a on lineaarliikme kordaja
arv b - vabaliige.

Võrdelise seose graafik on sirge, mis läbib alati punkti (0; 0).

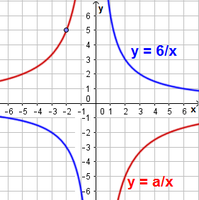
Pöördvõrdelise seose graafik on kahest harust koosnev hüperbool.

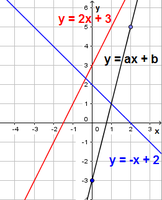
Lineaarfunktsiooni graafik on sirge, mis lõikab y-telge punktis (0; b).

NÄIDE 1: - leiame musta värvi graafiku puhul kordaja a väärtuse

Valime graafikul ühe täisarvuliste koordinaatidega punkti, näiteks (3; 3). Kuna ${{y \over x} = a}$, siis ${a = {3 \over 3} = 1}$.
Seega on must sirge seose y = x graafik.

 NÄIDE 2: - leiame punast värvi graafiku puhul kordaja a väärtuse

Valime graafikul ühe täisarvuliste koordinaatidega punkti, näiteks (-2; 5). Kuna xy = a, siis a = -2·5 = -10.
Seega on punane hüperbool seose ${y = -{10 \over x}}$ graafik.

 NÄIDE 3: - leiame musta värvi graafiku puhul kordajate a ja b väärtused

Graafik lõikab y-telge punktis (0; -3), seega b = -3.
Valime lisaks graafikul ühe täisarvuliste koordinaatidega punkti, näiteks (2; 5) ja leiame a väärtuse seosest 5 = a·2 - 3, ehk a = 4.
Seega on must sirge seose y = 4x - 3 graafik.