Parabool

PARABOOL - ruutfunktsiooni y = ax² + bx + c graafik

ax² - ruutliige; a - ruutliikme kordaja (a ≠ 0)
bx - lineaarliige; b - lineaarliikme kordaja
c - vabaliige

Kui a > 0, avaneb parabool ülespoole
Kui a < 0, avaneb parabool allapoole
Kui b = 0, asub haripunkt y-teljel
Parabool lõikab y-telge punktis (0; c)

.
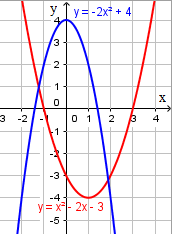
y = x² - 2x - 3
a = 1 > 0 - graafik avaneb ülespoole
c = -3, lõikepunkt y-teljega on (0, -3)

y = -2x² + 4
a = -2 < 0 - graafik avaneb allapoole
b = 0 - haripunkt asub y-teljel
c = 4 - lõikepunkt y-teljega on (0; 4).

Koht x-teljel, kus parabool lõikab või puudutab telge, on nullkoht.
Nullkohad on arvuliselt võrdsed vastava ruutvõrrandi ax² + bx + c = 0 lahenditega.

Parabool on sümmeetriline sirge suhtes, mida nimetatakse (sümmeetria)teljeks.
Parabooli ja selle telje lõikepunkt on haripunkt (x_h; y_h)
Parabooli sümmeetriateljeks on sirge x = x_h.

${x_h = -{b \over 2·a}}$

või (kui nullkohad x₁ ja x₂ leiduvad)

${x_h = {x_1 + x_2 \over 2}}$

y = x² - 2x - 3
a = 1, b = -2

${x_h = -{-2 \over 2·1} = {2 \over 2} = 1}$
Nullkohad: x₁ = -1; x₂ = 3
${x_h = {-1 + 3 \over 2} = {2 \over 2} = 1}$
Parabooli sümmeetriateljeks on sirge x = 1.

Parabooli haripunkti y koordinaadi y_h saab arvutades leida:

y_h = x_h² - 2x_h - 3 = 1² - 2 · 1 - 3 = 1 - 2 - 3 = -4.

Haripunkt: (1; -4)